-
[파이썬 | 알고리즘] 다익스트라 알고리즘(Dijkstra algorithm)IT Skils/알고리즘 2021. 4. 4. 13:08
지난번에는 탐욕 알고리즘(Greedy algorithm)에 대해 알아보았습니다.
이번에는 다익스트라 알고리즘(Dijkstra algorithm)에 대해 알아보겠습니다.
다익스트라 알고리즘(Dijkstra algorithm)
다익스트라 알고리즘이란 최단 경로 문제의 일부이며, 하나의 정점에서
다른 모든 정점 간의 각각 가장 짧은 거리를 구하는 알고리즘이다.
다익스트라 알고리즘(Dijkstra algorithm)의 접근법
heaq 라이브러를 이용해 우선순위 큐를 생성하고,
우선순위 큐에 저장되어있는 정점(첫 정점)을 추출하여,
추출 된 정점과 해당 정점에서 각 인접노드로 향하는 정점까지의 거리를 비교한다.
이때 각 인접노드는 배열에 저장되어있고, 각 인접노드로 가는 거리가 배열에 저장
(첫정점 =0, 이외정점 'inf =무한대로 초기화) 되어있는 길이보다 짧으면 배열에 해당
노드의 거리를 업데이트한다. 그 후 업데이트 되어 진 노드와 거리를 우선순위 큐에 넣는다.
우선순위 큐 (Heapq 라이브러리)
import heapq queue = [] heapq.heappush(queue, [2, 'A']) heapq.heappush(queue, [5, 'B']) heapq.heappush(queue, [1, 'C']) heapq.heappush(queue, [7, 'D']) print (queue) for index in range(len(queue)): print (heapq.heappop(queue))
우선순위 큐 Heqpq테스트 결과 우선순위 큐를 이용하기 위해 Heapq 라이브러리를 사용한다.
push 시 데이터가 heqp구조로 저장이 되며 pop을 했을 때 최소 값
부터 먼저 추출이 된다.

패턴 분석
●dictionary를 이용해 각 정점(key)마다 연결되어 있는 정점(node)과 거리(distance)를 저장한다.(
graph = {
'A': {'B': 8, 'C': 1, 'D': 2},
'B': {},
'C': {'B': 5, 'D': 2},
'D': {'E': 3, 'F': 5},
'E': {'F': 1},
'F': {'A': 5}
}1. 초기화: 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장
⎿ 초기에는 첫 정점의 거리는 0, 나머지는 무한대('inf') 저장
⎿ 초기에는 우선순위 큐에 첫 정점만 (거리 0) 넣는다.
거리 저장 배열 우선순위 큐 A B C D E F A 0 inf inf inf inf inf 0 2. 우선순위 큐에서 추출 한 정점(A, 0)과 인접한 점들과의 거리 계산
⎿ 첫 정점과 인접한 각각의 점들에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 저장되어있는 배열에서의 거리를 비교
⎿ 배열에 저장되어 있는 거리 > 첫 정점에서 해당 노드로 가는 거리 -> 해당 정점의 거리 배열에 업데이트 및 우선순위 큐에 push
⎿ 배열에 저장되어 있는 거리 < 우선순위에서 추출 한 정점의 거리 -> continue
●우선순위 큐 -> (A,0) 추출 // A와 인접한 정점 case1) B, 8 < inf -> update & 우선순위 push
거리 저장 배열 우선순위 큐 A B C D E F B 0 8 inf inf inf inf 8 ●우선순위 큐 -> (A,0) 추출 // A와 인접한 정점 case2) C, 1 < inf -> update & 우선순위 push
거리 저장 배열 우선순위 큐 A B C D E F C B 0 8 1 inf inf inf 1 8 ●우선순위 큐 -> (A,0) 추출 // A와 인접한 정점 case3) D, 2 < inf -> update & 우선순위 push
거리 저장 배열 우선순위 큐 A B C D E F C D B 0 8 1 2 inf inf 1 2 8 3.첫번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (C, 1)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (C, 1) -> 인접한 정점 B or D
⎿ 배열에 저장되어 있는 거리 > (A -> C -> B or D) -> 배열에 (A -> C -> B or D) 거리 update & 우선순위 큐 push
⎿ 배열에 저장되어 있는 거리 < (A -> C -> B or D) -> continue
●우선순위 큐 -> (C, 1) 추출 // 인접한 정점 case1) B, 5 // A -> C (1) -> B (5) = 6 < 8 update & 우선순위 큐push
거리 저장 배열 우선순위 큐 A B C D E F D B B 0 6 1 2 inf inf 2 6 8 ●우선순위 큐 -> (C, 1) 추출 -> 인접한 정점 case2) D, 2 // A -> C (1) -> D (2) = 3 > 2 -> continue
4.두번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (D, 2)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (D, 2) -> 인접한 정점 E or F
⎿ 배열에 저장되어 있는 거리 > (A -> D -> E or F) -> 배열에 (A -> D -> E or F) 거리 update & 우선순위 큐 push
⎿ 배열에 저장되어 있는 거리 < (A -> D -> E or F) -> continue
● 우선순위 큐 -> (D, 2) 추출 // case1) A -> D -> E 거리 5 < inf -> update & 우선순위 push
거리 저장 배열 우선순위 큐 A B C D E F E B B 0 6 1 2 5 7 5 6 8 ● 우선순위 큐 -> (D, 2) 추출 // case2) A -> D -> F 거리 7 < inf -> update & 우선순위 push
거리 저장 배열 우선순위 큐 A B C D E F E B F B 0 6 1 2 5 7 5 6 7 8 5.세번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (E, 5)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (E, 5) -> 인접한 정점 F
⎿ 배열에 저장되어 있는 거리 > (A -> E -> F) -> 배열에 (A -> E -> F) 거리 update & 우선순위 큐 push
⎿ 배열에 저장되어 있는 거리 < (A -> E -> F) -> continue
● 우선순위 큐 -> (E, 5) 추출 // case1) A -> E -> F 거리 6 < 7 -> update & 우선순위 push
거리 저장 배열 우선순위 큐 A B C D E F B F F B 0 6 1 2 5 6 6 6 7 8 5.네번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (B, 6)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (B, 6) -> 인접한 정점 X -> continue
● 우선순위 큐 -> (B, 6) 추출 // 정점 B에는 인접한 정점 X ->continue
거리 저장 배열 우선순위 큐 A B C D E F F F B 0 6 1 2 5 6 6 7 8 6. 다섯번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (F, 6)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (F, 6) -> 인접한 정점 A
⎿ 배열에 저장되어 있는 거리 > (A -> F -> A) -> 배열에 (A -> F -> A) 거리 update & 우선순위 큐 push
⎿ 배열에 저장되어 있는 거리 < (A -> F -> A) -> continue
● 우선순위 큐 -> (F, 6) 추출 // case1) A -> F -> A 거리 11 > 7 -> continue
거리 저장 배열 우선순위 큐 A B C D E F F B 0 6 1 2 5 6 7 8 7. 여섯번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (F, 7)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (F, 7) -> 인접한 정점 A
⎿ 배열에 저장되어 있는 거리 > (A -> F -> A) -> 배열에 (A -> F -> A) 거리 update & 우선순위 큐 push
⎿ 배열에 저장되어 있는 거리 < (A -> F -> A) -> continue
● 우선순위 큐 -> (F, 7) 추출 // A -> F 거리 -> 7, 이미 배열에 A -> F 최단거리 -> 6 인 상황 -> continue
거리 저장 배열 우선순위 큐 A B C D E F B 0 6 1 2 5 6 8 8. 일곱번 째 루틴 종료, 우선순위 큐가 MinHeap (최소 힙) 방식이므로, 우선순위 큐에서 (B, 8)이 먼저 추출(pop)
⎿ 우선순위 큐 추출 (B, 8) -> 인접한 정점 X -> continue
● 우선순위 큐 -> (B, 8) 추출 // 정점 B에는 인접한 정점 X & A -> B 거리 -> 8, 이미 배열에 A -> B 최단거리 -> 6인 상황 ->continue
거리 저장 배열 우선순위 큐 A B C D E F 0 6 1 2 5 6 우선순위 큐에서 더 이상 추출 할 데이터가 없다면 다익스트라 알고리즘 구현 완료
다익스트라 알고리즘 구현 (파이썬 | Dijkstra algorithm)
mygraph = { 'A': {'B': 8, 'C': 1, 'D': 2}, 'B': {}, 'C': {'B': 5, 'D': 2}, 'D': {'E': 3, 'F': 5}, 'E': {'F': 1}, 'F': {'A': 5} }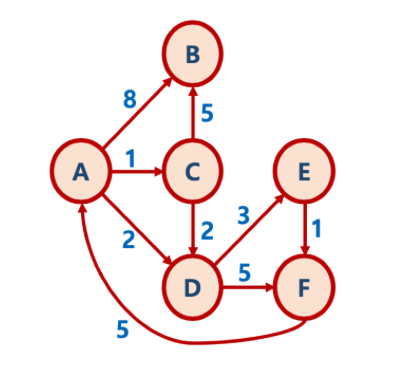
import heapq #우선순위 큐 def dijkstra(graph, start): #다익스트라를 위한 그래프와 첫 정점을 입력으로 받는다. distances = {node: float('inf') for node in graph} #각 정점들의 거리 inf로 초기화 distances[start] = 0 #첫 정점은 0으로 초기화 prioityqueue = [] #우선순위 큐 생성 heapq.heappush(prioityqueue, [distances[start], start]) #우선순위 큐에 첫 정점(A)과 거리(0)push while prioityqueue: #우선순위 큐에서 더 이상 추출 할 데이터가 없을 때 까지 current_distance, current_node = heapq.heappop(prioityqueue) #우선순위 큐 pop (거리가 젤 작은 점을 추출) #초기에는 첫 정점(A)과 거리(0)가 추출 됨 if distances[current_node] < current_distance: #추출 된 정점의 거리가 배열에 저장되어 있는 거리 보다 크면 continue #다음 루틴(다음 while문) 실행 #추출 된 정점의 거리가 배열에 저장되어 있는 거리 보다 작으면 for adjacent, weight in graph[current_node].items(): #추출 된 정점의 인접한 점들을 순회 distance = current_distance + weight #추출 된 정점의 거리 + 인접노드까지의 거리를 새로운 distance 저장 if distance < distances[adjacent]: #해당 점까지의 새로운 distance가 배열에 저장되어 있는 점까지의 distance보다 작으면 distances[adjacent] = distance #배열에 해당 점까의 거리 update heapq.heappush(prioityqueue, [distance, adjacent]) #해당 점까지의 거리를 우선순위 큐에 Push return distances #다익스트라가 완료 된 배열 리턴dijkstra(mygraph, 'A')
다익스트라 알고리즘 코드 테스트 테스트 결과
다익스트라 알고리즘 구현 코드가 정상적으로 구현됨
이상으로 [파이썬 | 알고리즘] 다익스트라 알고리즘 에 대해 알아보았습니다,
'IT Skils > 알고리즘' 카테고리의 다른 글
[파이썬 | 알고리즘] 크루스칼 알고리즘(Kruskal's algorithm) (0) 2021.04.11 [파이썬 | 알고리즘] 탐욕 알고리즘(Greedy algorithm) (0) 2021.03.26 [파이썬 | 알고리즘] 깊이 우선 탐색(Depth-First Search) (0) 2021.03.25 [파이썬 | 알고리즘] 너비 우선 탐색(Breadth-First Search) (0) 2021.03.25 [파이썬 | 알고리즘] 순차 탐색(Sequential Search) (0) 2021.03.21